Collections

 

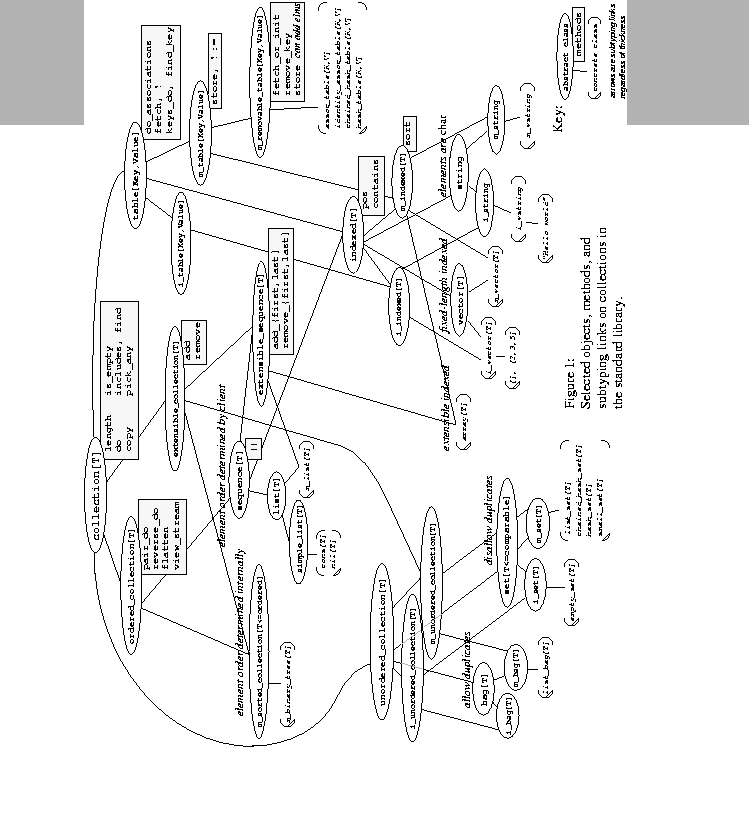
In collection.cecil:

Collections are groups of elements. We first introduce abstract interfaces, describing and refining various kinds of collections and their operations. We then shift to discussing concrete implementations which can be instantiated and manipulated at runtime.

There are three major families of collections: unordered collections (like bags and sets), ordered collections (e.g., lists), and tables (or keyed collections). Indexed collections like arrays, vectors, and strings are both ordered collections and keyed tables, where the keys are integer indices.

Abstract collection classes typically come in three versions: generic, immutable, and mutable, with the latter two indicated by i_ and m_ prefixes. For example:

abstract object indexed[`T] isa table[int,T], indexed[`S >= T];
abstract object i_indexed[`T] isa indexed[T];
abstract object m_indexed[`T] isa indexed[T];

This troika of versions of each abstraction is a standard idiom among the collection classes. A generic base class defines the abstract read-only behavior of the object, but doesn't specify whether the collection is mutable. One subclass adds the immutability specification, and another subclass adds the mutator operations. An immutable collection may contain mutable objects that are side-effected while in the collection, but the collection itself cannot be changed.

There are three varieties of mutation: replacement (removing one element but inserting another in its place), insertion (increasing the collection's size), and deletion (making the collection smaller). The latter two capabilities are captured by the abstract extensible_collection[T] and removable_collection[T] objects, which may be inherited by mutable objects.

Separating the read-only from the read-write interfaces (e.g., unordered_collection vs. m_unordered_collection) supports useful subtyping relationships among the read-only interfaces. To support the most reuse, the generic read-only interface should be used as a type declaration whenever possible. Only if mutation is required should the mutable subtype interface be used. The immutable interface must be distinguished from the generic read-only interface because the mutable interface cannot be a subtype of the immutable interface, considering the behavior specification implied by the immutable interface.

For a given abstraction, e.g., indexed, both the immutable and mutable versions containing elements of type T (or subtype of T) subclass the generic version with elements of type T or any supertype of T. In addition, the immutable version, i_indexed[T], is a subtype of any immutable collection (of the same kind) of a supertype of T:

extend type i_indexed[`T] subtypes i_indexed[`S >= T];

In contrast, a mutable version of a type T has no subtyping relation to a mutable collection with a different element type, e.g., m_indexed[int] is unrelated to m_indexed[num] : m_indexed[int] cannot have floats stored in it (unlike m_indexed[num]), and so m_indexed[int] is not a subtype of m_indexed[num]. Also, m_indexed[num] can contain things other than ints and reveal this through do, pick_any, etc. (unlike m_indexed[int]), so the reverse subtyping relation doesn't hold, either.

Finally, the immutable and mutable versions subclass those of the abstraction higher in the class hierarchy:

extend i_indexed[`T] isa i_table[int,T];
extend m_indexed[`T] isa m_table[int,T];