INDRIYATI
ATMOSUKARTO
CSE576 PROJECT 1: FEATURE DETECTION AND MATCHING
THURSDAY, 14 APRIL 2005
Project objective
Detect discriminating
features is an image (in this case edges and corners) and find the best
matching features in other images.
The features should be invariant to translation, rotation, illumination
and scale.
Feature Detection
Identify interest points in the image using Harris corner
detection method
Algorithm:
Convert image to greyscale
Apply Gaussian convolution to blur the image and
remove noise
Calculate gradient of image in x and y direction for
every pixel
For each point in the image, consider a 3x3 square
window of pixels
around that point.
Compute the
Harris matrix H for that point, defined as 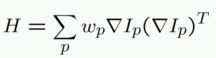 where the
summation is over all pixels in the window.
where the
summation is over all pixels in the window.
Compute the
corner strength
function 
Choose points whose c(H)
is above threshold and c(H) is local maxima in a 10x10
neighborhood.
These points will be called the feature points
(Current threshold is set at 0.001)
Feature description
1. A simple window descriptor
For each feature points
Take a 45x45 window centered at the
feature point
Normalise the color of each pixels in
the window
Make a 9x9 window feature
descriptor by doing a pyramid sampling for every 5 points
The feature
descriptor will contain the RGB value of the points, hence in total our
feature descriptor has 9x9x3 dimensions
Sum up the RGB
values separately of every 5 points in the window by applying linear
weights to the 5 points.
2. A simplified version of MOPS
For each feature points
Calculate the principal gradient
direction of the point by using its Harris matrix to find the
eigenvector and eigenvalue of the matrix
Take a 45x45 window centered at the
feature point
Rotate the window using
the feature point as the pivot of rotation and using the principal
gradient direction as the angle of rotation
Make a 9x9 feature
descriptor by doing pyramid sampling for every 5 points
Sum up the RGB values of every 5 points
in the rotated window by applying linear weights to the 5 points
The feature descriptor will be 9x93x dimensions
* I actually also tried a simpler version of the SIFT feature
(the code is still there it's just that the function is not called)
I didn't include it because after running the benchmark
test I saw that it was performing worse than simplified MOPS
so I chose simplified MOPS as my second descriptor
For each feature points,
Calculate principal
gradient direction of the point by using its Harris matrix to find the
eigenvector and eigenvalue of the matrix
So here you would have
used a window to find the Harrix matrix
For each of the pixels in
the above window find their individual gradient by taking their
derivatives
Calculate the difference
between each of the window pixel's individual gradient to the principal
gradient direction
Bin the difference into
one of 8 bins where bin0 is represents 0 to 45 degrees difference to
principal gradient, bin1 is for 45 to 90 and so on
So in total our feature
vector will have 8 dimensions
Feature matching
1. Use Euclidean
distance to calculate the distance between two feature descriptor and
apply a threshold
This matching measure is not very good because the
threshold is so subjective (finding a perfect threshold is an art)
and you actually need to change it for each
dataset, so I wouldn't recommend it at all.
2. Use Euclidean distance to calculate the distance between two feature
descriptor and then apply a threshold on the
ratio of the best distance matched to the second
best distance matched.
This matching measure is much better than applying a
direct threshold. We still use a threshold here but it's a ratio
threshold
and it gives a pretty good result for all the test
cases without tweaking it here and there. Currently set at 0.5 which
basically
means if the second best distance method is at least
twice as much as the first distance then that's good enough for a match.
* I actually tried doing sum of absolute difference but the performance
wasn't much different from doing Euclidean distance.
I also tried doing normalized cross correlation but
that didn't do well at all, could have been a mistake in my
implementation though.
Why
make such a descriptor?
Simple window
A window descriptor is the simplest possible descriptor. The window descriptor
is normalised so that the feature descriptor is more or less
invariant to changes in illumination.A sampling of a bigger window is
taken to allow some pixel inaccuracy.
Rotated window
To create a rotation invariant feature descriptor we have to take
into account the relative orientation of the features and align
the features so that we can match them across images.
Performance on benchmark images
Average pixel error:
Testcase
|
Feature Descriptor 1
|
Feature Descriptor 2
|
SIFT
|
Leuven
|
51.23
|
303.65
|
12.48
|
Graf
|
284.83
|
201.24
|
161.5
|
Bike
|
204.05 |
217.34
|
24.91
|
Wall
|
195.67 |
262.08
|
81.37
|
Note this performance measure depends on few factors: repeatability of
the feature detector, the descriptor and the matching.
Also averaging out may not be very fair because if you look at the
first few image pairs (image1-image2, image1-image3,
image1-image4) the simple descriptor does not bad but for the last two
images where the transformation is always
so extreme, there is a huge jump in error and averaging out kind of
misses this point. Also. for panoramic
stitching applications I don't think there would be any extreme
transformations between images.
To get the SIFT averages I ran testSIFTMatch for each of the 5 image
pairs (1-2,1-3,1-4,1-5,1-6) and averaged them.
The simple window descriptor which was assume to only do well in
translated images, can actually handle
some degree of rotations, sometimes even better than the so-called
rotation invariant descriptor.
For Leuven test case, the simple window descriptor performs well
because the images in Leuven have illumination changes
and very little transformation and since the window descriptor is
normalised then change of illumination is taken care of.
Strength and weakness
Strength:
The simple window descriptor is invariant to translation and
since each pixel in the feature window are normalised then
the descriptor is also invariant to illumination. In addition doing
sampling at every 5 pixels instead of taking
the whole bigger window will allow some inaccuracy in pixels.
The rotated window descriptor is slightly invariant to rotation
Weakness:
The descriptor does not perform as well as SIFT features.
The descriptor is not invariant to scale changes and major rotations
Pictures
Yongjoon, Seth and I went up to level 6 to take these pictures
with a tripod.

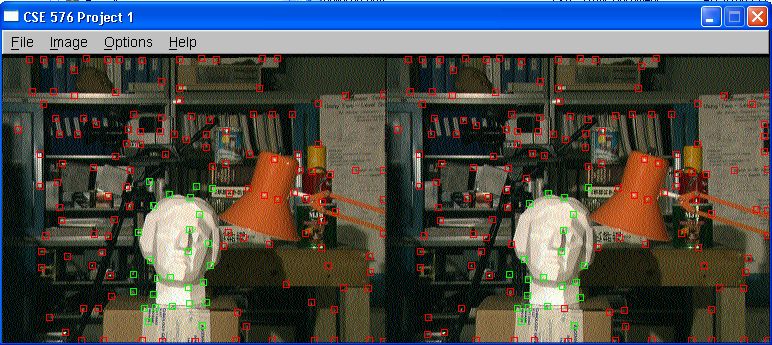
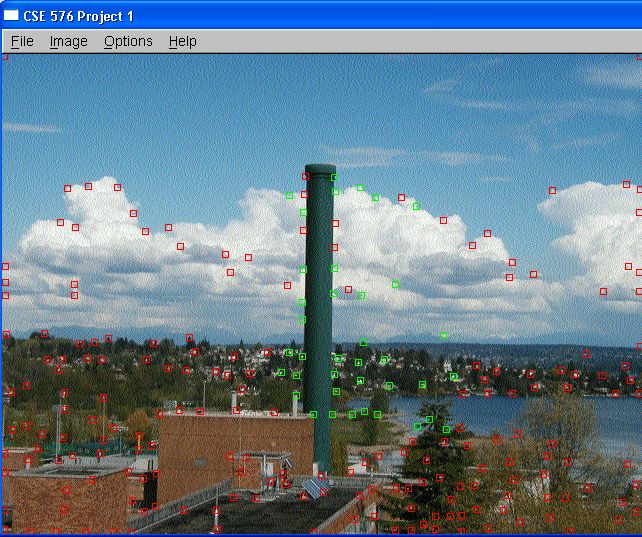
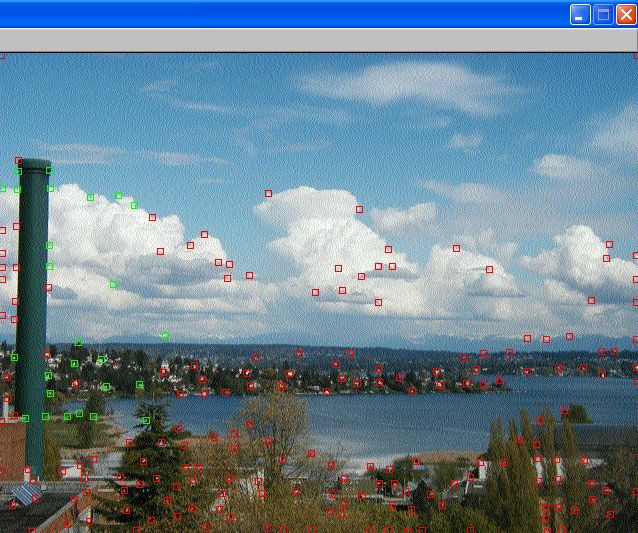
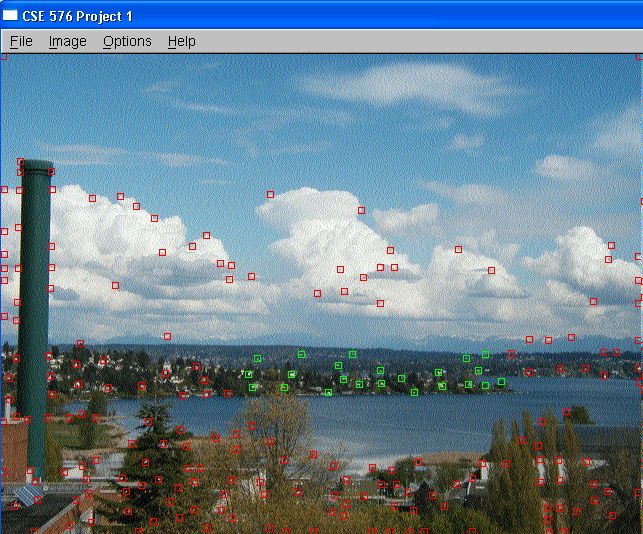
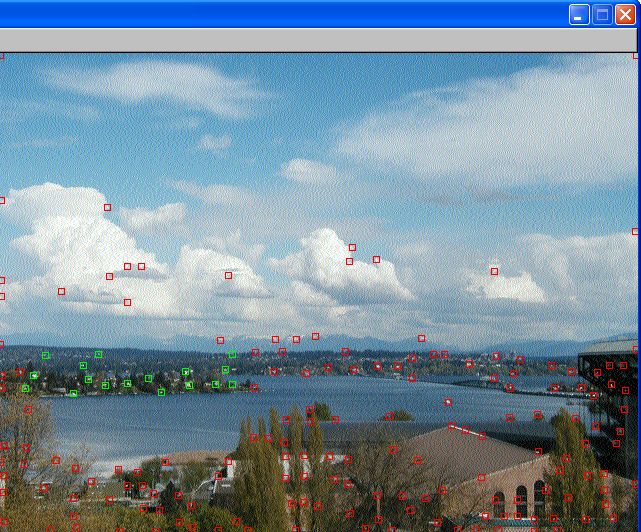
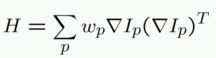 where the
summation is over all pixels in the window.
where the
summation is over all pixels in the window.





